从20世纪50年代开始，翻身陀螺这一精巧有趣的小玩具便引起了诸多学者的关注。早期的研究主要是从物理上定性分析，大多数学者均认为陀螺翻身是由摩擦引起的。1963年，Contensou在线性摩擦假设下对翻身陀螺进行了严格的动力学分析，成功解释了陀螺翻身的原理。杨海兴、成功在1993年应用部分变量稳定性定理导出了翻身陀螺解析形式的稳定性判据。还有学者利用数值仿真方法研究了陀螺翻身的条件。2007年，刘延柱对翻身陀螺的发明过程及研究历史进行了梳理，并从物理概念出发简明清晰地分析了陀螺翻身的力学原理。作者从小就喜欢玩各式各样的陀螺，其中翻身陀螺最为独特，如图 1，它的两端是两个不同半径的大小球面，陀螺重心与两个球面的球心都不重合且在大球球心的下方，静止时大球在下，短柄朝上，与不倒翁类似，但旋转起来之后，陀螺会奇迹般地翻身，变为短柄朝下、大球朝上的旋转。在玩翻身陀螺的过程中，作者产生了很多疑问，其中一些疑问通过阅读上述文献得到了解释，下面我们尝试解答剩下另外几个疑问。

问题1. 翻身过程中角速度怎么变？会不会翻过头？

       陀螺翻身是因为有摩擦力的作用，这是学术界所公认的。当陀螺进动速度较大时，摩擦力对陀螺质心的力矩会使陀螺与垂直方向的夹角变大，进而出现翻身现象。那么陀螺翻身过程中的角速度会怎么变呢？会不会翻过头呢？

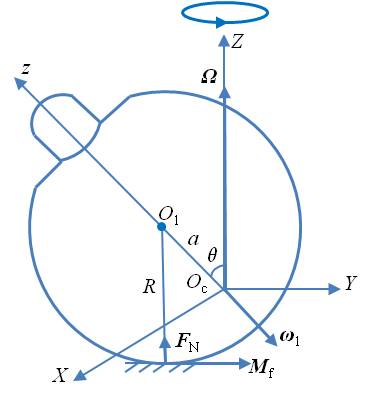
图 1翻身陀螺正立状态

       如图 1为陀螺正立时的状态，建立以陀螺质心O_c为原点的惯性坐标系（O_c-XYZ），i，j，k分别为X、Y、Z轴的单位矢量。以质心O_c为原点建立陀螺主轴坐标系（O_c-xyz），z轴为陀螺对称轴，θ为z轴与竖直方向的夹角。由于陀螺关于z轴对称，设其绕主轴x、y、z的主转动惯量分别为A、A、C。则陀螺进动时所受摩擦力矩的水平分量为

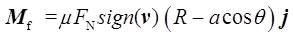
其中μ为动摩擦系数，F_N为地面支撑力的大小，v为陀螺与地面接触点相对地面的滑动速度，R为大球半径，a为质心与大球圆心的距离。

      摩擦力矩引起章动角θ变化，产生一个附加动量矩，该动量矩以进动角速度Ω绕垂直轴旋转会引起一个附加陀螺力矩。根据文献的推导，该附加陀螺力矩为

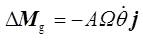
ΔM_g与M_f相平衡，大小相等，方向相反。由此可以得出陀螺翻身的角速度大小

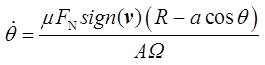
其中，滑动速度v的大小为

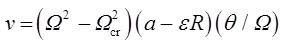
Ω_cr为进动角速度的临界值，ε = ( C – A ) / C，由于C与A接近，所以ε为小量。只有当陀螺进动角速度Ω大于临界值Ω_cr时，v的方向才为正， 大于0，陀螺作“翻身”运动。随着章动角θ增大， 也会增大， 陀螺“翻身”加快，直至完全倒立。

        至此，有人可能会担心：陀螺会不会翻身太快，翻过头了，又翻回去？其实，这是多虑了，当陀螺完全倒立后，它与地面的接触方式发生改变，陀螺不再遵循上述运动规律，而是属于刚体定点运动的Lagrange情况，即倒立陀螺作进动。也就是说，陀螺到达倒立状态时有些“剩余”速度，相当于在普通陀螺高速旋转时被横推一下，陀螺只是从直立转动状态变成进动。

问题2. 进动与自转的方向“相反”？

       当陀螺在地上旋转受到干扰时，会发生进动而不倒下，这便是陀螺的进动性。大多数普通陀螺在地面上进动时，俯视陀螺，其进动方向与自转方向是一致的，均为顺时针或者逆时针旋转，如图 2(a)所示。而翻身陀螺却不一样，当俯视翻身陀螺的进动时，其进动方向与自转方向是“相反”的，如图 2(b)。

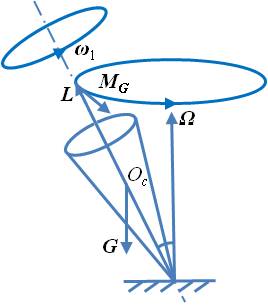
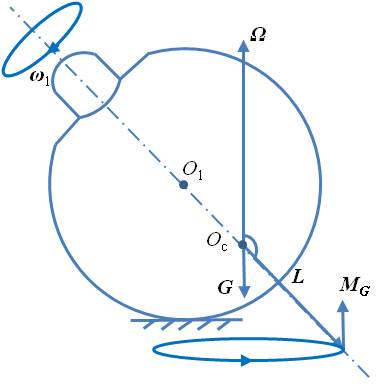
(a)普通陀螺的进动                                                                    (b)翻身陀螺的进动

图 2普通陀螺与翻身陀螺的进动现象比较

        对此，我们可以从物理概念上作如下分析。在图 2(a)中，假定普通陀螺的自转方向是逆时针，根据陀螺近似理论，动量矩L的方向可认为与自转角速度ω₁方向一样，当陀螺受扰倾斜时，重力G与法向约束力F_N构成力偶，其力偶矩M_G垂直纸面向外，使得陀螺发生进动。根据莱查定理，力偶矩方向与动量矩矢端的速度方向一致，动量矩L矢端的运动轨迹如图 2(a)所示，沿逆时针方向旋转，即陀螺的进动方向也是逆时针。在图 2(b)中，假定翻身陀螺的自转方向是顺时针，动量矩L的方向同样认为与自转角速度ω₁方向相同，当其受扰倾斜时，重力G与法向约束力F_N构成力偶，其力偶矩M_G垂直纸面向里，这一点与普通陀螺恰恰相反，其动量矩L矢端的运动轨迹如图 2(b)所示，沿逆时针方向旋转，可得翻身陀螺的进动方向是逆时针，这就解释了翻身陀螺的进动方向与自转方向为何是“相反”的。

       这种有趣的现象，在力学上其实也有严格的证明。当主转动惯量A < C时，可以证明陀螺的进动角速度与自转角速度之间为钝角，也就是我们所讨论的俯视时进动与自转方向“相反”，而翻身陀螺刚好符合这个条件。

问题3. 自转越快越易翻身吗？

       当旋转普通陀螺时，可以发现旋转得越快，陀螺就越稳定，这也正是陀螺定轴性的体现，因此，很多人在玩陀螺时，就会下意识地用力旋转，使陀螺快速转动。推及到翻身陀螺，大家同样也会尽可能地用力旋转，以期使陀螺翻身。然而事实却并非如此，笔者大量实验的结果表明，翻身陀螺并不是自转的越快就越易翻身，而是在自转角速度小到一定程度时才会翻身，即使初始时自转角速度很大，翻身陀螺也会正立旋转一段时间，直到自转角速度降下来之后才会翻身。

       对于这种现象，我们可以用陀螺近似理论进行分析。在陀螺近似理论中，通过简单的推导，我们可以得出陀螺的进动角速度为

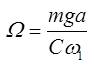
其中，ω₁表示自转角速度的大小。根据上文的分析，欲使陀螺翻身，Ω则必须大于临界值Ω_cr，因而可以得出

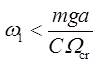
即当陀螺的自转角速度小于某值时，陀螺才会翻身，这一结果与翻身陀螺的旋转实验吻合。

结束语

       翻身陀螺是一件小的玩具，关于它的趣味问题却不少，除了陀螺翻身以及本文发现的趣味现象以外，仍有许多值得思考的地方。本文研究的翻身陀螺是翻转180^o的情况，在生活中也存在一些类似现象，但是只翻转90^o，例如，扁平触地的图钉、纽扣或围棋子，在特定转速下可以自己立起来，水平旋转的熟鸡蛋也可能自己立起来。地球是近似的椭球体，运动与翻身陀螺有类似之处，有学者根据地质勘探的结果推测地球曾经发生过90^o翻转。这些翻转现象，与翻身陀螺的机理有何异同呢？这很值得深入研究。另外，还有一些与前述不同的趣味现象，比如在立起过程中鸡蛋会短暂跳起，鸡蛋在旋转的过程中可能形成两种稳定状态：以较细的一头直立旋转，或者以较粗的一头直立旋转。如果能研究清楚这些奇怪而有趣现象的力学机理，那才算是真的会玩呐。