1 自然界中的波浪云
2011 年12 月16 日清晨,某观察者在美国阿拉巴马州伯明翰市(Birmingham, Alabama,USA) 拍摄到一组高大,顶部呈弧线的“恐龙云”(好像一群迁徙的长颈恐龙) 整齐一致地在地平线上缓慢行进(图1). 当时,不明缘由的人们纷纷向气象局询问,并担心其可能预示着某种灾难. 其实,这是一种普遍存在的自然现象——开尔文--亥姆霍兹波浪云(Kelvin-Helmholtz wave clouds),又名“波浪云”(图2). 微风拂过,湖面泛起层层波浪,也是这一现象;而其幕后“黑手”不是某种灾难,实为流动稳定性理论中的开尔文--亥姆霍兹不稳定性;甚至画技精湛的大师文森特·梵高亦或受这一现象启发,而成名作《星月夜》.

图1 美国阿拉巴马州伯明翰市波浪云
(视频:http://www.youtube.com/watch?v=VDlkl8vhK1c)

图2 自然界中的波浪云(侧视)
(更多图片:http://www.my7475.com/27239.html)
笔者也时而能观察到这一“波浪云”现象(图3).

图3 自然界中的波浪云(仰视)
2 开尔文--亥姆霍兹不稳定性现象
流动稳定性理论研究流体运动稳定的条件和失稳后流动的发展变化,包括转捩为湍流的过程.层流向湍流转捩,一般始于失稳. 但随着某流动参数(如雷诺数) 逐渐增大,流动失稳后也可能过渡为另一种更复杂的层流,而不一定转捩为湍流,继续多次,最终失去层流的规律性,转捩为湍流. 朗道(Lev Davidovich Landau,1908--1968 年) 称之为“重复分岔”. 本文介绍的开尔文--亥姆霍兹不稳定性问题是两种不同流体有一个明确界面时的稳定性问题之一(另一种被称为瑞利--泰勒稳定),实际上它发生在流动转捩为完全无规则湍流之前.
2.1 开尔文--亥姆霍兹不稳定性的定义
开尔文--亥姆霍兹不稳定性(Kelvin-Helmholtz instability)是一种在有剪切速度的连续流体内部或有速度差的两种不同流体的交界面之间发生的不稳定性现象. 它使得该交界面扭曲,形成规律形态. 而这一现象先后被德国物理学家、生理学家赫尔曼·冯·亥姆霍兹(Hermann von Helmholtz,1821 年8 月 31 日--1894 年9 月8 日) 和英国数学物理学家威廉·汤姆逊·开尔文勋爵(William Thomson, 1st Baron Kelvin,1824 年6 月26 日--1907 年12 月17 日) 发现并解释,故被称为开尔文--亥姆霍兹不稳定性. 这种不稳定性现象常见于云、海洋(图4(a))、土星的云带(图4(b))、木星的大红斑(图4(c))、太阳的日冕中. 近来研究表明:存在于平行分界面流速方向的磁场,对沿流速方向的小扰动有致稳作用;当两种流体流速差引起的失稳作用大于磁场的致稳作用时,磁流体力学领域中也会出现这一不稳定性现象.
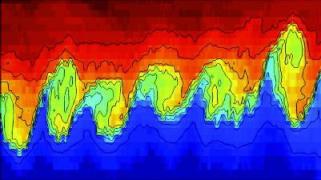
(a) 大西洋深500m处因开尔文--亥姆霍兹不稳定性产生的波浪
(来自:Lgostiau)

(b) 土星大气层内因两条云带相互作用引发的开尔文--亥姆霍兹
不稳定性现象(来自:NASA)

(c) 木星红斑中的开尔文--亥姆霍兹不稳定性现象(来自:NASA)
图4
2.2 原理及其流动可视化
根据前文定义,如图5 所示,不同密度的无黏均匀流体作平行于水平界面的相对运动,假设其各自所占空间在各方向上都伸展至无穷远. 按照流体运动稳定性理论中的小扰动理论(又称线性理论):若密度1小于密度2,当不计此时界面表面张力时,界面都是不稳定的;当考虑界面表面张力,重力加速度,则相对速度满足一定条件时不稳定. 若考虑理查逊数(Ri),则当Ri< 0.25 时,该界面运动失稳.
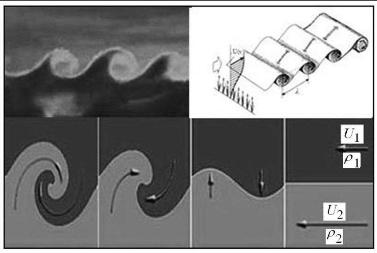
图5 开尔文--亥姆霍兹不稳定性波浪云的形成过程
据此,当两个不同的温度空气团(层) 以不同速度(不计方向性) 移动时,就具备了形成”开尔文--亥姆霍兹波浪云”的必要条件. 前面我们观察到的“波浪云”很可能便是由于近地面风速较慢处有冷空气层(即云或雾),其在移动过程中遇到位置较高、较为温暖的高速空气层,当两个空气层的物理参数满足上述开尔文-- 亥姆霍兹不稳定性条件后形成的交界面运动失稳,并向湍流转捩的现象.
我们明白了开尔文--亥姆霍兹不稳定性现象的形成原理和条件,就可以用流动可视化技术重现这一有趣的现象. 图6中,先在水槽中准备好上下两层不同比重的液体:上部透明层为清水,下部蓝色层为比重1.012 的盐水. 当把水槽倾斜与水平面呈10°之后,短时间内可以观察到开尔文--亥姆霍兹不稳定性现象. 而正因为这一失稳过程甚为短暂,故而前文中描述的那排完美连续的“恐龙云”仅在几分钟内形成并很快消散,让人不禁诧异:鱼能蹦出水面,波浪(云) 居然也可以,堪称奇观.

图6 开尔文--亥姆霍兹不稳定性的流动可视化
(视频:http://www.youtube.com/watch?v=q3K-XcWiDE)
2.3 开尔文--亥姆霍兹不稳定性的作用
开尔文--亥姆霍兹不稳定性会使得流体运动失稳,引起运动状态由层流向湍流转捩,进而流体动量交换加剧,能量耗散加快,摩擦阻力增加. 常见于水面碎浪和蒸发率突然增加.
3 类开尔文--亥姆霍兹不稳定现象
3.1 一般类开尔文--亥姆霍兹不稳定现象
除了前文例举的开尔文--亥姆霍兹不稳定现象,实验室和神秘的自然界中还存在着诸多“类开尔文--亥姆霍兹不稳定”(Kelvin-Helmholtz-like in-stability)现象. 例如,实验时流体运动在规则排列的立方体粗糙元壁面、多孔壁面、可渗透介质壁面之上;自然界植被群落表面、城市建筑物群上方空气运动所呈现出的不稳定流动过程及期间所形成的“类开尔文-- 亥姆霍兹波浪云”结构.
3.2 梵高《星月夜》



